Jenseits von Raum und Zeit

Unser derzeitiges Verständnis der fundamentalen Naturkräfte beruht auf den beiden Grundpfeilern Quantenfeldtheorie und Relativitätstheorie, die in den jeweiligen Anwendungsbereichen Elementarteilchenphysik und Astrophysik/Kosmologie mit sehr hoher Genauigkeit getestet und bestätigt sind. Bei extrem hohen Energiedichten (unmittelbar nach dem Urknall oder im Zentrum schwarzer Löcher) benötigen wir allerdings eine Synthese der zugrundeliegenden Prinzipien, da hier weder Quanten- noch Raumkrümmungseffekte vernachlässigt werden können. Dies stellt uns vor neue konzeptuelle Probleme, da die Anwendung der quantenmechanischen Unschärferelation auf die Schwerkraft (Gravitation) und damit direkt auf die Raum-Zeit Geometrie letztendlich bedeutet, daß (zumindest klassische) geometrische Vorstellungen bei "kleinsten Abständen" nicht mehr angemessen sind.

Die Stringtheorie ist ein Kandidat für eine konsistente Quantentheorie der Gravitation und führt zugleich zu einer natürlichen Vereinigung mit den anderen Elementarteilchenkräften. Sie macht es wahrscheinlich, daß sich in einem Zwischenbereich (bevor der Begriff der Raum-Zeit-Geometrie sinnlos wird) die effektive räumliche Dimension erhöht und die nicht-gravitativen Naturkräfte als Krümmungseffekte in den unsichtbaren Dimensionen verstanden werden können. Während die Idee einer sehr kleinen fünften Dimension als geometrische Erklärung für Elektrizität und Magnetismus schon seit den 20er Jahren existiert, brachte die quantenmechanische Dualität verschiedener Stringtheorien die neuartige Vorstellung mit sich, daß unsere beobachtbare Raum-Zeit nur eine niedrigdimensionale Kompenente in einem höherdimensionalen Kontinuum sein könnte.

Eine Schranke an die Energie, die benötigt wird, um eine solche fünfte Dimension zu beobachten, kann aus der Energiebilanz der Supernova SN1987A hergeleitet werden. Dies ist ein Beispiel dafür, wie die Physik der kleinsten Bausteine der Materie auf Zusammenhänge mit der Physik der Sterne (Astrophysik) und mit der Struktur des Universums im Großen (Kosmologie) führt.

Quantenfeldtheorie

Im subnuklearen Bereich werden Materie und Kräfte durch Quantenfelder beschrieben; das sind, anschaulich gesprochen, aus Energiepaketen zusammengesezte Kraftfelder. Diese Objekte haben sowohl Wellen- als auch Teilchencharakter und entziehen sich unserer durch makroskopische Phänomene geprägten Anschauung. Sie sind uns nur im Rahmen mathematischer Konzepte faßbar, deren Anfänge an den Beginn des 20. Jahrhunderts zurückreichen und die noch immer Gegenstand intensiver Forschung sind.

Die Quantenfeldtheorie bildet die Grundlage für unser theoretisches Verständnis der Elementarteilchen und ermöglicht, von der Annahme lokaler (punktförmiger) Wechselwirkungen ausgehend, die Berechnungen der Kräfte zwischen den Materieteilchen. Der (in der klassischen Näherung) punktförmig gedachte Wechselwirkungsbereich führt allerdings zu Unendlichkeiten, die im Fall der Gravitation die direkte Feldquantisierung inkonsistent machen. Den einzigen bekannten Ausweg bildet die Stringtheorie, in der die elementaren Freiheitsgrade nicht mehr punktförmig sind.

Allgemeine Relativitätstheorie (Schwerkraft/Gravitation)

Ausgehend von der Massenunabhängigkeit der Bewegung im Gravitationsfeld gelang es Einstein, auf der Grundlage des vierdimensionalen Raum-Zeit Kontinuums der speziellen Relativitätstheorie die Wirkung der Gravitation als Krümmung dieses Kontinuums zu verstehen. Die Veränderlichkeit der Raum-Zeit Geometrie, deren Quelle die Materieverteilung ist, hat drastische Konsequenzen. Ihre spektakulärste ist wohl die Existenz von kausal getrennten Raum-Zeit Regionen, den Schwarzen Löchern. Unter Vernachlässigung von Quanteneffekten kann Materie zwar in ein Schwarzes Loch eindringen, es jedoch nicht wieder verlassen. Dies ist mit einer Vergrößerung der entkoppelten Region und damit ihrer Begrenzung (dem Horizont) verbunden.

Die physikalischen Gesetze, welche das Verhalten von (stationären) Schwarzen Löchern beschreiben, weisen eine große Ähnlichkeit mit den Gesetzen der Thermodynamik (Wärmelehre) auf. Daß diese Gesetze tatsächlich thermodynamischen Ursprungs sieht man allerdings erst nach (partieller) Einbeziehung von Quanteneffekten: Aufgrund des sogenannten Hawking-Prozesses emittiert ein Schwarzes Loch Strahlung einer definiten Temperatur. Ein mikroskopisches Verständnis der damit verbundenen Entropie erfordert allerdings eine über die Quantisierung der Materiefelder hinausgehende echte Quantentheorie der Gravitation.

Unschärferelation, Raum und Zeit

Die Quantentheorie lehrt uns, daß die Energie (bzw. der Impuls) von "Materiewellen" nur in ganzzahligen Vielfachen einer Grundquantität vorkommen können, die proportional zur Frequenz (bzw. zur Wellenzahl) ist. Da nun mögliche Testobjekte selbst diesen Gesetzen gehorchen müssen, folgt, daß Energie und Zeit (bzw. Impuls und Ort) zusammen nie beliebig genau gemessen werden können (Heisenberg'sche Unschärferelation). Ausgehend von der Ruheenergie E=mc2 eines Elementarteilchens ergibt sich somit eine Zeitunschärfe und, als Weg, den das Licht in dieser Zeit zurücklegt, die "Comptonwellenlänge" (die natürliche Größeneinheit für die Ortsunschärfe eines Punktteilchens der Masse m).

Wenn wir nun die Schwerkraft in unsere Überlegung einbeziehen, so bildet ein (naiv betrachtet) punktförmiges Elementarteilchen ein Schwarzes Loch, dessen Schwarzschild-Radius mit der Masse wächst, während die Compton-Wellenlänge kleiner wird. Bei der sogenannten Planckmasse von ungefähr 1019GeV/c2 (das ist etwa 1019 mal die Masse eines Protons, bzw. 1016 mal die höchste in Teilchenbeschleunigern erzielte Energie) rutscht nun die Comptonwellenlänge eines Punktteilchens in seinen eigenen Horizont (der gerade mal 10-33cm erreicht hat, ein 1020-stel der Größe eines Atoms!), sodaß hier der Unterschied zwischen Elementarteilchen und Schwarzem Loch verschwimmt und die Raum-Zeit Geometrie prinzipiell nicht mehr vermessen werden kann. (Der "kürzeste Augenblick" wäre dann die Zeit, die das Licht braucht, um diese sogenannte Plancklänge zurückzulegen.)

Wegen dieser fundamentalen Unschärfe ist dann die Frage nach den "kleinsten" Bausteinen der Materie in ihrer ursprünglichen Form nicht mehr sinnvoll und muß durch neue Konzepte ersetzt werden. Die entsprechende extrem hohe Energie pro Teilchen kann auch in eine Temperatur umgerechnet werden, die im Universum nur unmittelbar nach dem Urknall (etwa 10-40 Sekunden lang) herrschte. Aus den Quantenfluktuation in der darauffolgenden Epoche sind vermutlich auch die Dichteschwankungen entstanden, die im weiteren Verlauf der kosmischen Entwicklung zur Bildung von Galaxien und Galaxienhaufen führten.

Stringtheorie

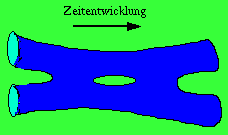Die elementaren Freiheitsgrade der Stringtheorie sind eindimensionale Objekte (strings = Saiten = Fäden mit Spannung). Wie eine eingespannte Saite besitzen sie Grund- und Oberschwingungen. Ihre (quantisierten) Schwingungsmoden werden nun mit den Elementarteilchen identifiziert. Wie im Bild gezeigt, können diese Ojekte wechselwirken, indem sich die durch ihre Zeitentwicklung im Raum-Zeit Kontinuum überstrichenen Flächen (die sogenannten Weltflächen) in einem kontinuierlichen Prozeß vereinigen und wieder aufspalten. So vereinheitlicht die Stringtheorie sowohl die verschiedenen Typen von Elementarteilchen (als Schwingungszustände eines fundamentalen Objekts) als auch deren verschiedene Wechselwirkungen (durch die einfache Dynamik der zweidimensionalen Weltfläche im Raum-Zeit Kontinuum).

Die Erweiterung der Wechselwirkungspunkte der Teilchenphysik zu glatten Wechselwirkungsbereichen liegt der Konsistenz der Stringtheorie bei kleinen Abständen zugrunde. Konsistenz bei großen Abständen erfordert Supersymmetrie (Superstrings) und erklärt damit auch die Existenz der Fermionen (etwas vereinfacht können wir die Fermionen = Fermi-Teilchen mit Materie und die Bose-Teilchen mit Kraftfeldern identifizieren).

Bei sehr großer Spannung werden die "Fäden" sehr kurz (man kann hier an die Plancklänge denken, obwohl die Längenskala der Stringtheorie durchaus auch wesentlich größer sein könnte), und wir sehen bei entfernter Betrachtung nur noch die punktförmige Wechselwirkung punktförmiger Elementarteilchen.

Fünf (und mehr) Dimensionen

Kaluza und Klein haben 1921 und 1926 vorgeschlagen, den Elektromagnetismus im Rahmen der allgemeinen Relativitätstheorie als Krümmungseffekt in einer sehr kleinen fünften Dimension aufzufassen. Diese Idee läßt sich theoretisch auf sehr ansprechende Weise realisieren, fand aber ein halbes Jahrhundert lang wenig Beachtung, weil eine experimentelle Überprüfung ihrer Konsequenzen nicht möglich war. Erst mit der Konstruktion der supersymmetrischen Erweiterung der Gravitationstheorie (SUGRA=Supergravitation) und der Frage, ob erweiterte und/oder höherdimensionale Supersymmetrie die Inkonsistenz der Quantengravitation beheben kann, wurden diese Überlegungen wieder aktuell. Inzwischen waren allerdings die Kernkräfte entdeckt und, analog zum Elektromagnetismus, als Eichtheorien formuliert worden, sodaß eine geometrische Vereinheitlichung der Naturkräfte nunmehr zumindest ein 11-dimensionales Raum-Zeit Kontinuum erfordert. 11 ist aber zugleich die maximale Dimension, in der eine SUGRA existiert. Dieses Zusammentreffen weckte große Hoffnungen, die sich allerdings vorerst nicht erfüllten, weil auch die 11-dimensionale SUGRA an unheilbaren Divergenzen krankt.

In dieser Situation löste 1984 eine Arbeit von Green und Schwarz die erste Stringrevolution aus: Es stellte sich nämlich heraus, daß Superstrings automatisch auf eine konsistente 10-dimensionale SUGRA mit Paritätsverletzung führen (d.h. es gibt, wie in der Natur beobachtet, nur linksdrehende Neutrinos, aber keine rechtsdrehenden; die Konstruktion einer konsistenten SUGRA mit dieser Eigenschaft war bis dahin nicht gelungen). Die Superstringtheorie ist darüber hinaus die einzige bekannte Theorie, die eine Vorhersage für die Raum-Zeit Dimension liefert, und die Vorhersage ist D=10. Damit wurde aus der Idee von Kaluza und Klein viele Jahrzehnte später ein plausibles Szenario: Wir leben in einer zehndimensionalen Welt.

Inzwischen hat sich allerdings die Palette der Möglichkeiten noch erweitert, denn Fortschritte im Verständnis von Quantenphänomenen in Stringtheorien lösten 1995 die zweite Stringrevolution aus: Es stellte sich nämlich heraus, daß die (Typ IIA) Stringtheorie im Bereich starker Kopplung eine zusätzliche Dimension generiert, sodaß (nun unter dem Namen "M-Theorie") die elfte Dimension zu neuen Ehren kam.

Nicht nur über die Zahl der verborgenen Dimensionen, sondern auch über ihre Größe ist noch nicht das letzte Wort gesprochen: Aus Dualitäten zwischen den fünf verschiedenen 10-dimensionalen konsistenten Stringtheorien haben wir nämlich gelernt, daß die unsichtbaren Dimensionen nicht unbedingt klein sein müssen, sondern daß die für uns beobachtbare Raum-Zeit Physik möglicherweise auf (geladenen) "3-dimensionalen Membranen" (sogenannten "Dirichlet branes") in einem höherdimensionalen Kontinuum lokalisiert ist. Diese Objeke sind konsistente Lösungen der effektiven zehn- bzw. elfdimensionalen String-Bewegungsgleichungen und führen zu großen Quanteneffekten, die frühere Vorhersagen der String-Phänomenologie drastisch modifizieren können.

In einem der untersuchten Szenarien wird zum Beispiel die Physik in einem energetischen Zwischenbereich zuerst 5-dimensional, bevor dann später alle 10 oder 11 Dimensionen ins Spiel kommen. Als Analogie kann man sich ein enges Tal vorstellen, aus dem man erst durch Aufwenden einer Mindestenergie entkommen kann. Entsprechend könnte sich die fünfte Dimension in hochenergetischen Prozessen der Elementarteilchenphysik bei Beschleunigerexperimenten, aber auch durch Abstrahlung von Gravitationswellen in der Energiebilanz von Supernovaexplosionen bemerkbar machen.

Dualität

Der Begriff der Dualität bedeutet in der Quantenfeldtheorie, daß Modelle mit unterschiedlichen klassischen Freiheitsgraden und/oder Kopplungsstärken auf äquivalente Quantentheorien führen und somit ein bestimmtes physikalisches Modell durch verschiedene klassische Ausgangspunkte realisiert werden kann, die sich nach der Quantisierung nicht mehr unterscheiden.

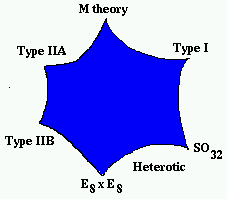In Unkenntnis der exakten Quantenkorrekturen ging man lange Zeit davon aus, daß es fünf verschiedene konsistente Superstringtheorien (in 10 Dimensionen) gibt: Typ I entspricht offenen Strings ("relativistische Schnüre mit freien Enden"), Typ IIA und IIB kommen, ebenso wie die beiden heterotischen Varianten mit Eichgruppen SO32 bzw. E8xE8, von geschlossenen Strings ("supersymmetrische Gummiringerl").

Als klassische Theorien lassen sich diese klar unterscheiden. Als exakte Quantentheorien sind sie aber vermutlich durch Variation gewisser Parameter (Vakuumerwartungswerte von masselosen Skalarfeldern, genannt Moduli) kontinuierlich miteinander verbunden. String-Dualitäten führen also zu der Vorstellung eines Kontinuums von Stringtheorien (genannt Moduliraum), deren Analyse uns aber derzeit nur in gewissen Grenzfällen möglich ist, in denen die exakte Quantentheorie gut genug durch eine klassische Beschreibung angenähert werden kann. Solche Grenzfälle sind, neben den fünf klassischen Superstring-Theorien und der M-Theorie, eine Vielzahl von niedrigerdimensionalen Modellen, die derzeit Gegenstand intensiver Forschung sind.

Der praktische Wert dieser Dualitätshypothese ist, daß man damit exakte Quantenkorrekturen in einer der genannten Stringtheorien durch eine klassische Rechnung ermitteln kann, die allerdings von anderen "elementaren Objekten" ausgeht (bis hin zu einer unterschiedlichen Dimension des zugrundegelegten Raum-Zeit Kontinuums). Mit derartigen Rechnungen wurde die Hypothese der Dualität aller konsistenten Stringtheorien in den letzten Jahren ausgiebig getestet und bestätigt.

Weiterführende Links & Informationen

Auf den folgenden englischsprachigen Web-Pages finden sich viele Informationen über String-Theorie und verwandte Gebiete für Laien und Spezialisten:
Allgemeine links zu Elementarteilchenphysik:

Last modified: April 25, 1999
by Maximilian.Kreuzer@tuwien.ac.at . [URL: http://hep.itp.tuwien.ac.at/~kreuzer]